Geometry and molecular motion

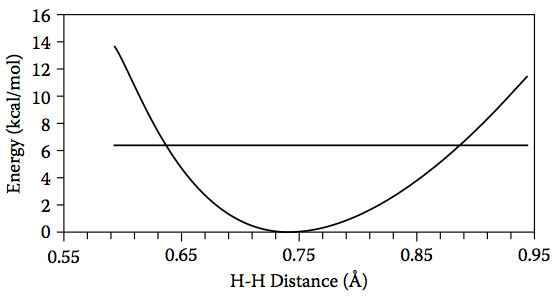
Figure 4.18. The relative energy of H2 as a function of H–H distance and the energy of the lowest vibrational level (horizontal line).
From Molecular Modeling Basics CRC Press, 2010

When discussing structure and other molecular properties it is important to remember that the molecule is in constant internal motion due to vibrational motion. The bond length and angles that one so carefully computes and reports to so many decimal places actually changes considerably with time.

Consider the H₂ molecule. Using B3LYP/6-31G(d) and the harmonic oscillator approximation, the frequency for the H–H stretch vibration is 4450 cm^–1, which corresponds to 6.4 kcal/mol of kinetic energy. If we compute the energy as a function of the H–H bond length (Figure 4.18), we see that this kinetic energy is enough to compress the H–H bond length to roughly 0.64 Å and increase it to 0.88 Å: the classical turning points.

The classical turning points can be estimated using the harmonic approximation of the potential energy surface (PES)
where ν_i is the vibrational frequency in units of cm^–1, with a corresponding normal coordinate l_i (see section 1.3 of the book), and n is the vibrational quantum number. Thus, ν_i = 4450 cm^–1 corresponds to a turning point at l_i =±0.087 amu^½ × Å which can be converted to Cartesian coordinates (and hence a bond length) using the normal mode component L_ij In the case of H₂, this gives classical turning points at 0.621 Å and 0.865 Å, which are in good agreement with the previous estimate from Figure 4.18. The screencast below shows ho MacMolPlt can be used to estimate the classical turning points.

For lower frequencies the displacements at the classical turning points can be quite substantial, both because the PES is flatter and because higher vibrational levels are populated. For example, in the case of ethane the lowest frequency is 310 cm^–1 [at the B3LYP/6-31G(d) level of theory] and corresponds mainly to rotation about the CC bond (Figure 4.20a). For the ground vibrational level the classical turning points occur at l_i =±0.330 amu^½ × Å , which corresponds to a dihedral angle change of ±14° (Figure 4.20b, see screencast below). At room T 4% of the ethane molecules have three quanta of energy in this mode (n = 2), corresponding to a kinetic energy of 2.2 kcal/mol, enough to change the dihedral angle by ±31°.

Figure 4.20. (a) Normal mode associated with the lowest frequency computed for ethane using B3LYP/6-31G(d). (b) Structure obtained by displacing along the mode by 0.330.
Click on the picture for an interactive version.
Click here for a pop-up window
From Molecular Modeling Basics CRC Press, 2010

Some of the lowest frequencies you’ll observe are for intermolecular interactions such as the water dimer hydrogen bond (Figure 4.22). Curious how much the geometry is displaced? Why not try it yourself? (See this post to get started with GAMESS).

Figure 4.22. (a) The PM3 normal mode corresponding to (a) torsional motion about the hydrogen bond and (b) hydrogen bond stretch in the water dimer. The corresponding frequencies are 128 and 415 cm^–1.
Click on the picture for an interactive version.
Click here for a pop-up window
From Molecular Modeling Basics CRC Press, 2010

Using MacMolPlt to compute the displaced geometry
As you can see from the second equation, the normal coordinate is basically a scale factor. Thus, MacMolPlt can be used to compute a displaced geometry by converting l_i to a percent and changing the units to amu^½ × Bohr by dividing by 0.52918 Å/Bohr. Thus, l_i =±0.330 becomes 62.0% (note that there is a mistake in the book: I forgot about the unit conversion in Figure 5.27). Unfortunately, MacMolPlt does not include the m^-½ so this is only an estimate.