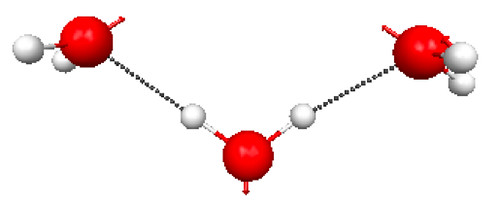
Figure 4.26. PM3 optimized structure of the V-shaped water timer. Shown also is the normal mode corresponding to the lowest vibrational frequency (36 cm–1).
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
While the lowest energy conformation of three water molecules is the ring structure (Figure 4.17), there is another minimum (at least on the PM3 potential energy surface - Figure 4.26) that is 7.7 kcal/mol higher in (electronic) energy.
The free energy difference between the cyclic and V-shaped structure is zero at around 480 K. This can be considered a very simple model for melting (i.e., the T at which higher enthalpy conformations are most probable because of entropy). The entropic term has two basic contributions: there are more higher-energy structures (they are more disordered so there are more ways to make them: e.g. there are 3 identical V-shaped structures), which lowers the conformational free energy, and the structures are “floppier” (they have more low-frequency vibrational modes), which lowers the vibrational free energy.
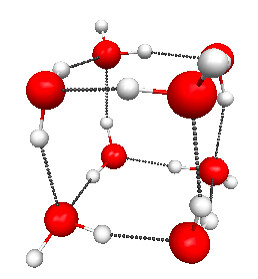
Figure 4.28a. Structure of one of the water clusters found by Maeda and Ohno. The coordinates are taken from their supplementary materials. (From S. Maeda and K. Ohno, 2007. Journal of Physical Chemistry A. 111: 4526–4534.)
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
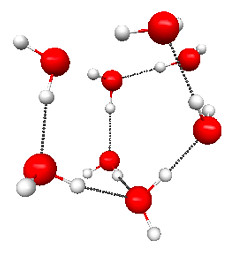
Of course, this is a hypothetical melting transition because the cyclic “ice” structure already sublimates at 285 K. The main reason for the high melting temperature is the small number of higher-enthalpy conformations, which increases quickly with the number of water molecules. For example, for water octamer [(H2O)8] a study by Maeda and Ohno found 164 different conformations, and only seven of these can be classified as some variant of the lowest-enthalpy cubic conformation (Figure 4.28a), while the rest are more disordered (e.g., Figure 4.28b). The study estimates that the temperature at which the cubic and more disordered structures become equally probable (i.e., the melting temperature) is around 280–320 K, which is significantly closer to the melting temperature of bulk ice of 273 K. The uncertainty in the estimate of Tmelt comes from the difficulty in estimating the effect of BSSE and anharmonic effects.
Figure 4.28b. Structure of one of the water clusters found by Maeda and Ohno. The coordinates are taken from their supplementary materials. (From S. Maeda and K. Ohno, 2007. Journal of Physical Chemistry A. 111: 4526–4534.)*
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
Click on the picture for an interactive version.
From Molecular Modeling Basics CRC Press, 2010
* The Jmol structure does not correspond exactly to the picture. When making the figure I forgot to write down which of the 164 structures I used for this figure. Still, the point is the same.




3 comments:
Hi
I know that my comment has no relationship with your post but I'm going to send this comment to you:
Your blog is great about using GAMESS and related software. But I think most of the new users have problem about installing GAMESS (like me). Please make a post about installing gammes on LINUX 64bit. Specially about preparing "rungms". I have problem about running gamess in parallel. I searched the net; i understood that many people have this problem but there is no answer for it. Please send a step by step guide for it. I'm sure it is useful for many people. I someone can not install a program, how he/she can use it.
Thank you
Alchemist: not a bad idea. Let me see what I can do.
The post can now be found here
Post a Comment