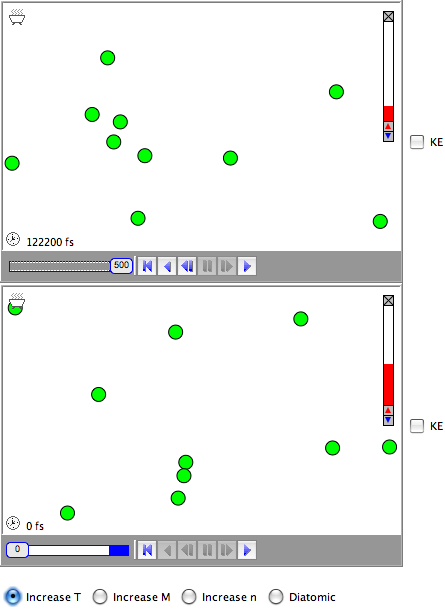
This screencast shows a Molecular Workbench model I made to illustrate the connection between internal energy and molecular motion (the model is included at the bottom of the post).
For a monatomic gas such as He or Ar the part of the internal energy (U) that depends on temperature (T) is
 and has only contributions from translational motion. Kinetic theory tells us that
and has only contributions from translational motion. Kinetic theory tells us that which, with a little algebra, gives us a direct connection between the internal energy and the average kinetic energy of the atoms in the gas:
which, with a little algebra, gives us a direct connection between the internal energy and the average kinetic energy of the atoms in the gas: You can see in the first container that while the internal energy reflects an average speed, the individual atoms can have very different speeds, which are constantly changing due to collisions. This can be illustrated by coloring the atoms according to the kinetic energies (red means more kinetic energy).
You can see in the first container that while the internal energy reflects an average speed, the individual atoms can have very different speeds, which are constantly changing due to collisions. This can be illustrated by coloring the atoms according to the kinetic energies (red means more kinetic energy).Increasing the temperature increases the internal energy and this is reflected in an increase in the average speed, as you can see by clicking on the "Increase T" button.
However, it is important to remember that the internal energy is a reflection of the kinetic energy, which is also a reflection of the mass. Thus, a heavier atoms will have the same internal energy and kinetic energy at the same temperature, but the atoms will move slower on average (the "Increase M" button).
Also, the internal energy can be increase by adding more particles, but this does not change the average speed of the molecules at the same temperature (the "Increase n" button).
The last ("Diatomic") button changes the atoms to diatomic molecules without changing the mass, i.e. the mass of the atoms in the second container are half that of the atoms in the first container. Because the mass is unchanged the average speed of the molecules (more precisely, of their center of mass) is the same as for the atomic gas at the same temperature, as is the translational internal energy (3/2nRT ).
However, notice that the molecules are also rotating, meaning they have additional (internal) energy compared to the atomic gas, which amounts to nRT (3/2nRT for non linear molecules):
 The internal energy also has a vibrational contribution (here the frequency is converted to a wavenumber, i.e. units of cm-1):
The internal energy also has a vibrational contribution (here the frequency is converted to a wavenumber, i.e. units of cm-1): though it is hard to make out the vibrational motion in the simulation. However, for most diatomic molecules this contribution is negligible at temperatures relevant to most chemists.
though it is hard to make out the vibrational motion in the simulation. However, for most diatomic molecules this contribution is negligible at temperatures relevant to most chemists.You can play around with the model yourself by clicking on the picture below, or on this web page, or you can download the model if you have Molecular Workbench installed on your computer. Enjoy!




1 comment:
excellent article, this will be a great resource for my upcoming paper on kinetic energy, thanks
Post a Comment