Canonical and localized molecular orbitals

Figure 4.10. 0.045 au isosurfaces of the four valence canonical MOs of NH₃ computed using B3LYP/6-31G(d). A value of 0.045 au is chosen because it results in a 0.002 au isodensity surface when squared.
From Molecular Modeling Basics CRC Press, May 2010.
Click on the picture for an interactive version

According to Valence Shell Electron Pair Repulsion (VSEPR) theory many bond angles involving elements such as C, N, and O are close to 109.5^o because the four valence electron pairs that surround these atoms adopt a tetrahedral geometry to minimize repulsion. In the case of CH₄ the H-C-H angle is exactly 109.5^o because the repulsion between the four electron pairs in the C-H bonds are identical. NH₃ has a lone pair that is fatter than a bond near the nucleus, so the lone pair-bond repulsion is slightly larger than the bond-bond repulsion. This results in a H-N-H angle of 107^o, slightly smaller than 109.5^o.

However, this is far from obvious when looking at the four valence MOs of NH₃ (Figure 4.10) computed using B3LYP/6-31G(d). The reason is that that MOs are not unique, and that these MOs (which lead to a diagonal Fock matrix and are known as canonical MOs) are not the MOs where the electron pair repulsion is a minimum. Algorithms have been implemented that find a new set of MOs (localized MOs or LMOs) that represent a linear combination of canonical MOs for which the MO–MO repulsion is a minimum (Figure 4.11).

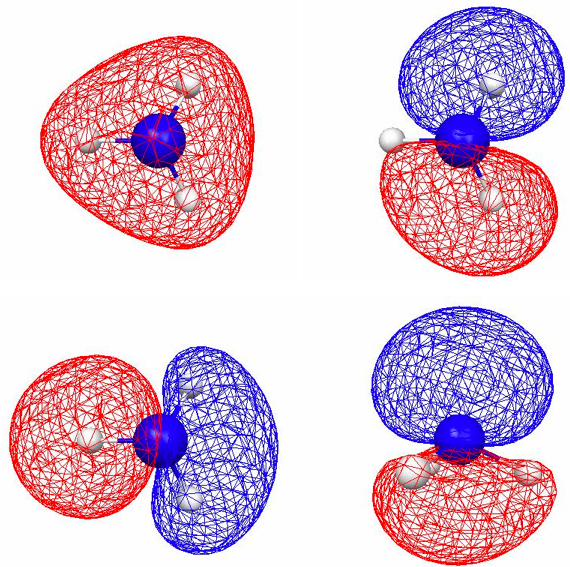
Figure 4.11. 0.045 au isosurfaces of the four valence localized MOs of NH₃ computed using B3LYP/6-31G(d). There are three N–H bond LMOs [(a)–(c)] and one lone pair LMO [(d)].
From Molecular Modeling Basics CRC Press, May 2010.
Click on the picture for an interactive version

LMOs for which the inter-orbital repulsion is a minimum are called energy localized orbitals or Edmiston-Ruedenberg orbitals. Other popular choices are Foster-Boys and Pipek-Mezey LMOs, which use different localization criteria.

Using MacMolPlt
The screencast below shows how to compute Ruedenberg LMOs for ammonia using GAMESS (local=ruednbrg in the $contrl group), and how to display the LMOs, as well as the canonical MOs, in MacMolPlt. I also show how to identify the HOMO and LUMO canonical MOs in MacMolPlt.

Note that I specify a geometry optimization in the GAMESS input file. GAMESS will only compute the LMOs for the optimized geometry.

Using Jmol
I use Jmol for the interactive figures and the scripts can be found here and here. Unlike the density and electrostatic potential, Jmol can generate its own grid data, so to display MO number 2 you simply use "mo 2" in the script. I use

mo 2; mo cutoff 0.045; mo fill nomesh; mo translucent 0.2

to make it a little prettier.

Jmol cannot find the MOs in a GAMESS geometry optimization file, and Jmol only stores the LMOs if present. So to display the canonical MOs with Jmol you need a single point energy calculation (output file) and to display the LMOs with Jmol you need a single point energy calculation with local=ruednberg added (output file).